When going through Gaussian blur, the input image I(x,y) is filtered as shown by eq. 1.

∞∑ ∑∞ 1 - i22+σj22- O (x,y) = 2π-σ2e G I(x + i,y +j) i=- ∞j=-∞ G
(1)

The Bienaymé’s identity states that

∑n ∑n V ar(∑ni=1Xi) = i=1 Var(Xi)+ i,j=1,i⁄=jCov (Xi,Xj )
(2)

Thus, the variance of a linear combination is:

∑ ∑ Var( ni∑=1ciXi) = ni=1 c2iV ar(Xi)+ 2× ni,j=1,i⁄=jcicjCov (Xi,Xj )
(3)

However, if Xi,...,Xn are pairwise independent integrable random variables 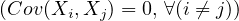(Cov (Xi, Xj) = 0, ∀(i ⁄= j)), which is our assumption in the following, then:

( ∑ ) ∑ Var ciXi = c2iV ar(Xi) i i
(4)

where ci are constants.

We consider that the variance of the input image is V ar[I(x + i,y + i)] = σ02, our goal here is to estimate the variance of the output (filtered) image V ar[O(x,y)] = σf2. Thus,

∞∑ ∑∞ ( - i2+j2)2 σ2f = σ20 --12-e 2σ2G j=- ∞ i=-∞ 2πσG
(5)

For large σG, the squared Gaussian is smooth and the sum can be approximated as:

∫∞ ∫∞ ( - i2+j22)2 σ2f ≈ σ20 -∞ -∞ 2π1σ2G-e 2σG di.dj 2 = 4σπσ02G-
(6)

and thus,

--σ0--- σf ≈ 2σG√ π-
(7)

In summary, when an image composed of Gaussian noise of standard deviation σ0 is being filtered by a Gaussian filter of standard deviation σG, the so-obtained filtered image has a standard deviation of σf according to the equation 7.

However, for our particular purpose, we intend to determine which Gaussian filter (of standard deviation σG) shall be used on the input image so as to obtain a filtered image with a given target statistics (σf), and hence σG ≈ σ0∕(2σf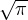√ -- π).