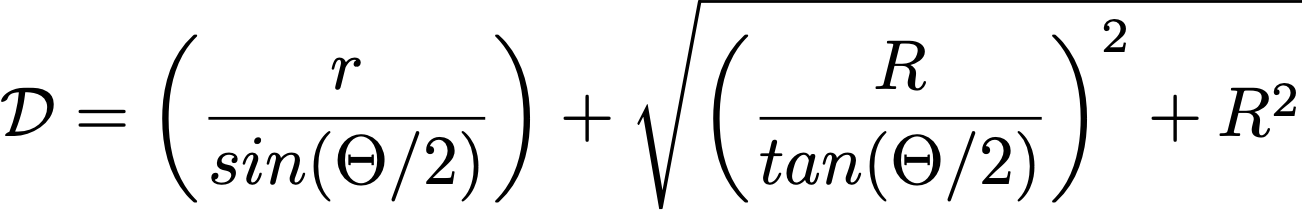Medical Imaging

Important note:

The work presented here is protected by

patent #EP 22305928.8,

submitted on June 27th 2022.

I am currently involved in a project with the neuro-radiology and interventional surgery departments of the University Hospital in Nantes. In the framework of this project, we have several aims.

We intend to :

Get an optimal segmentation of the cerebral vascular tree on MRA-TOF acquisitions.
Automatically recognize the 15 bifurcations of interest along the Circle of Willis.
Detect and segment Intra-Cranial Aneurysms (ICA).

Source code available there :

https://gitlab.univ-nantes.fr/autrusseau-f/vamos (synthetic model source code)
https://gitlab.univ-nantes.fr/autrusseau-f/ica-detection (aneurysm detection)

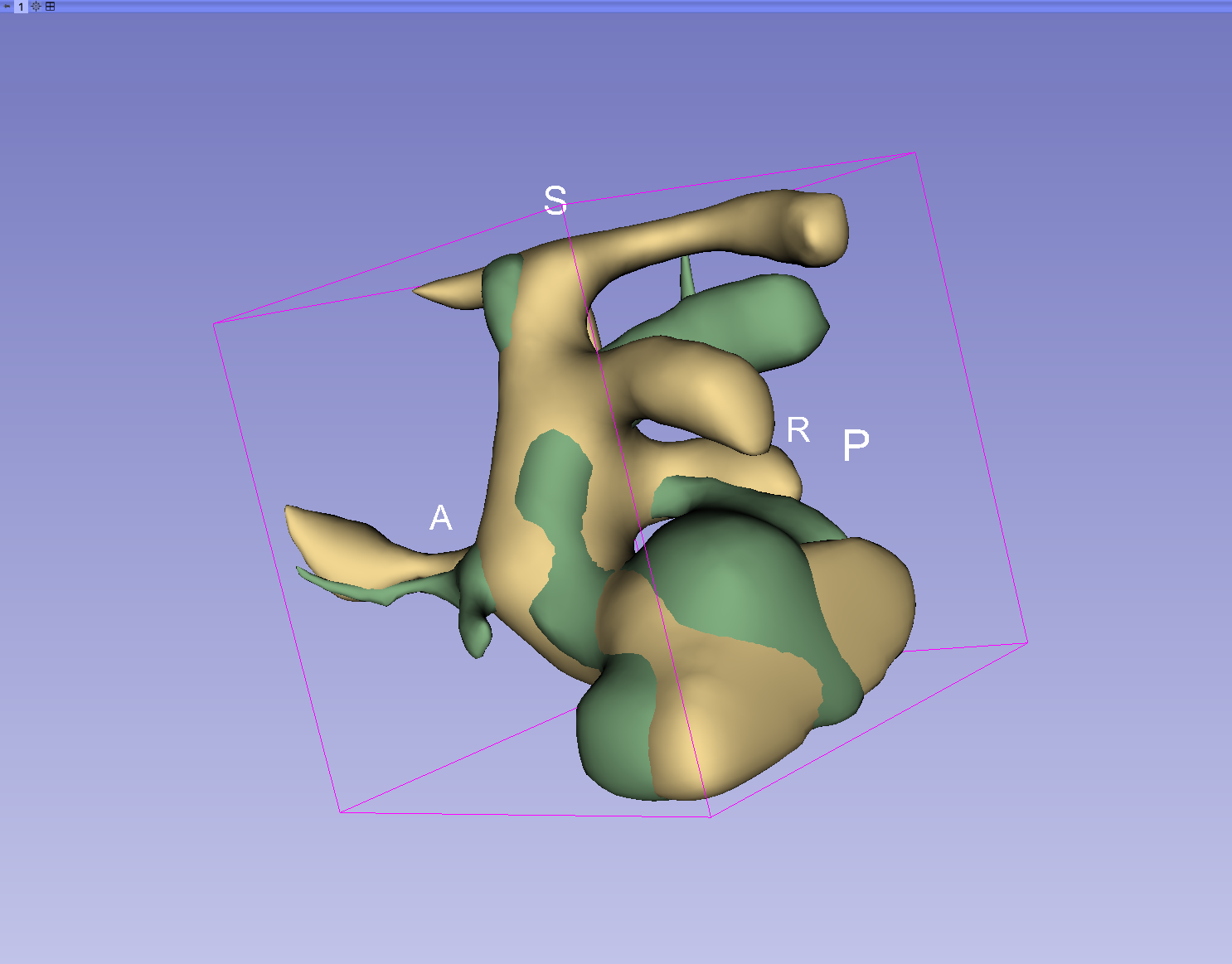
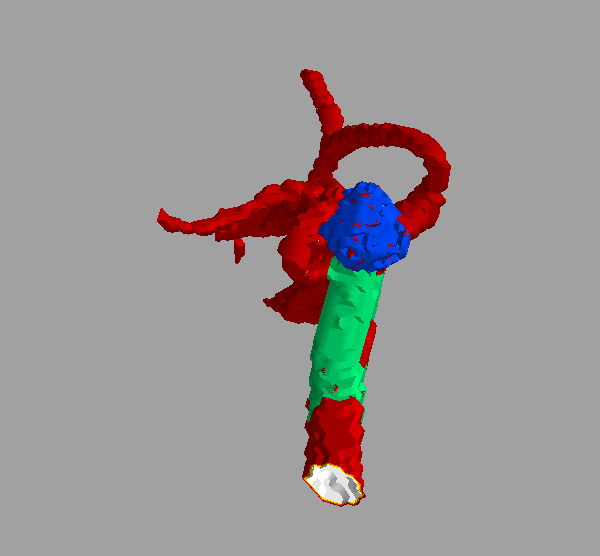
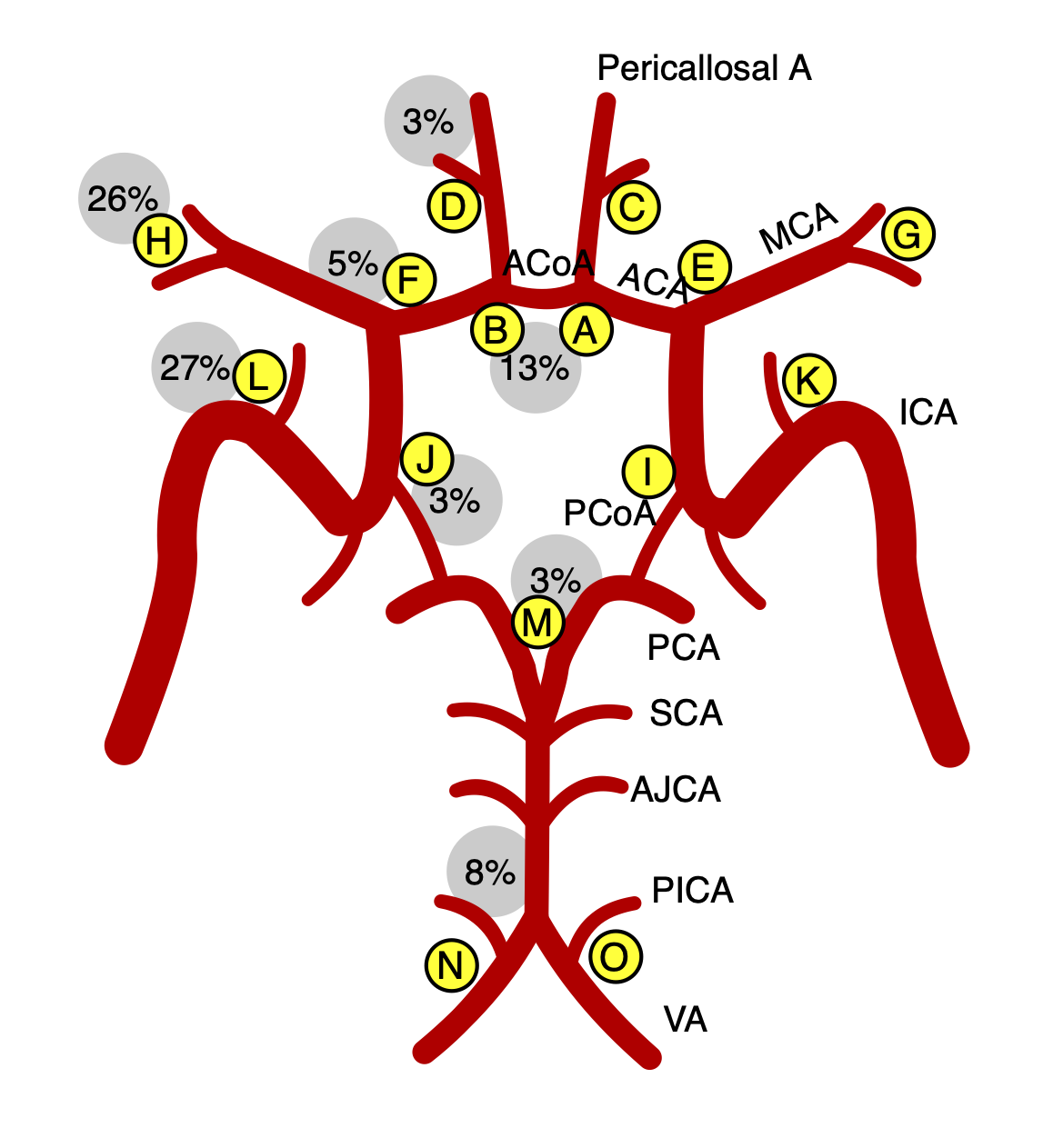
The ICAs commonly occur onto a specific portion of the vascular tree called the Circle of Willis (CoW). The figure below shows the layout of the CoW along with the 15 bifurcations of interest (yellow labels).

(Note : click on the figures to enlarge)

As far as deep learning methods are concerned in medical imaging (or most of the other applications) one of the greatest bottlenecks is the lack of training data.

Commonly, experts (neuro-radiologists in our case) are asked to manually label or segment numerous images, so that a CNNN can be trained on a given task. This manual segmentation/labeling task is very tedious and time consuming.

Our main objective in this project is to propose a synthetic model of the vascular tree. Such a model would allow to generate extremely high quality augmentation images, and hence allow to reduce the labeling burden while exhibiting very high performances.

Basically, this model aims to mimic as best as possible some portions of the vascular tree, and more precisely, the bifurcations of interest.

Our model exploits the spline functions to fit the arteries' centerlines. Some modifications of the spline coefficients, and of the convolution kernel (bringing some thickness to the modeled arteries) allows us to tweak a little bit the shape of the arteries.

The vascular model also includes a thorough analysis and modeling of the background noise. Hence, we can very accurately replicate any portion of the brain (as acquired on a MRA-TOF acquisition).

Thanks to our previous works, we have some tools to measure various features from the arterial tree bifurcations (see schematic representation below).

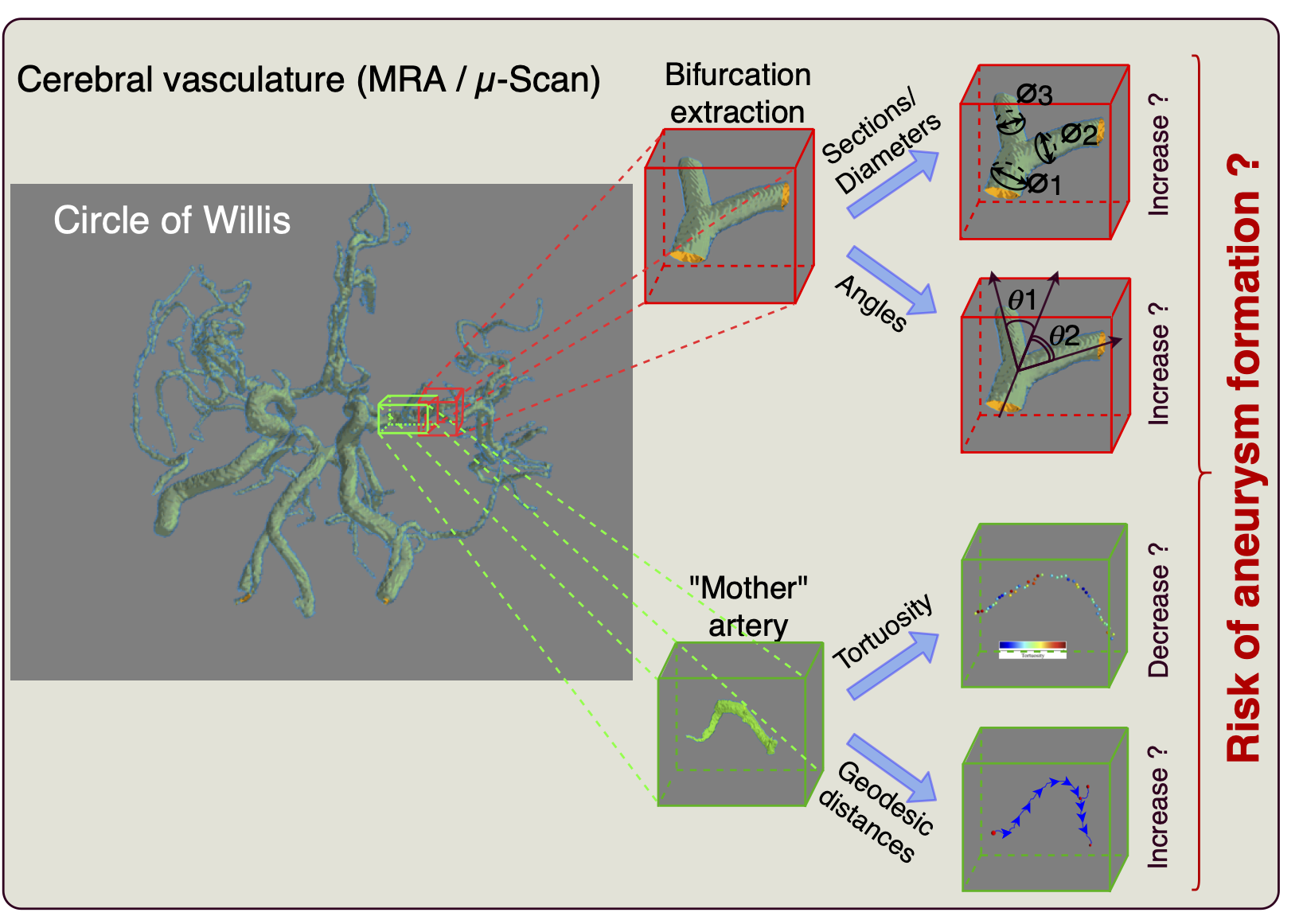
These geometric features are then used by the vascular model to mimic the arterial tree and moreover, some statistical properties of the background noise are also modeled.

The final goal of this model being to generate a significant amount of images for the training step of Convolutional Neural Networks, we first need to come up with a ground truth dataset. We have constituted a full image dataset including several areas.

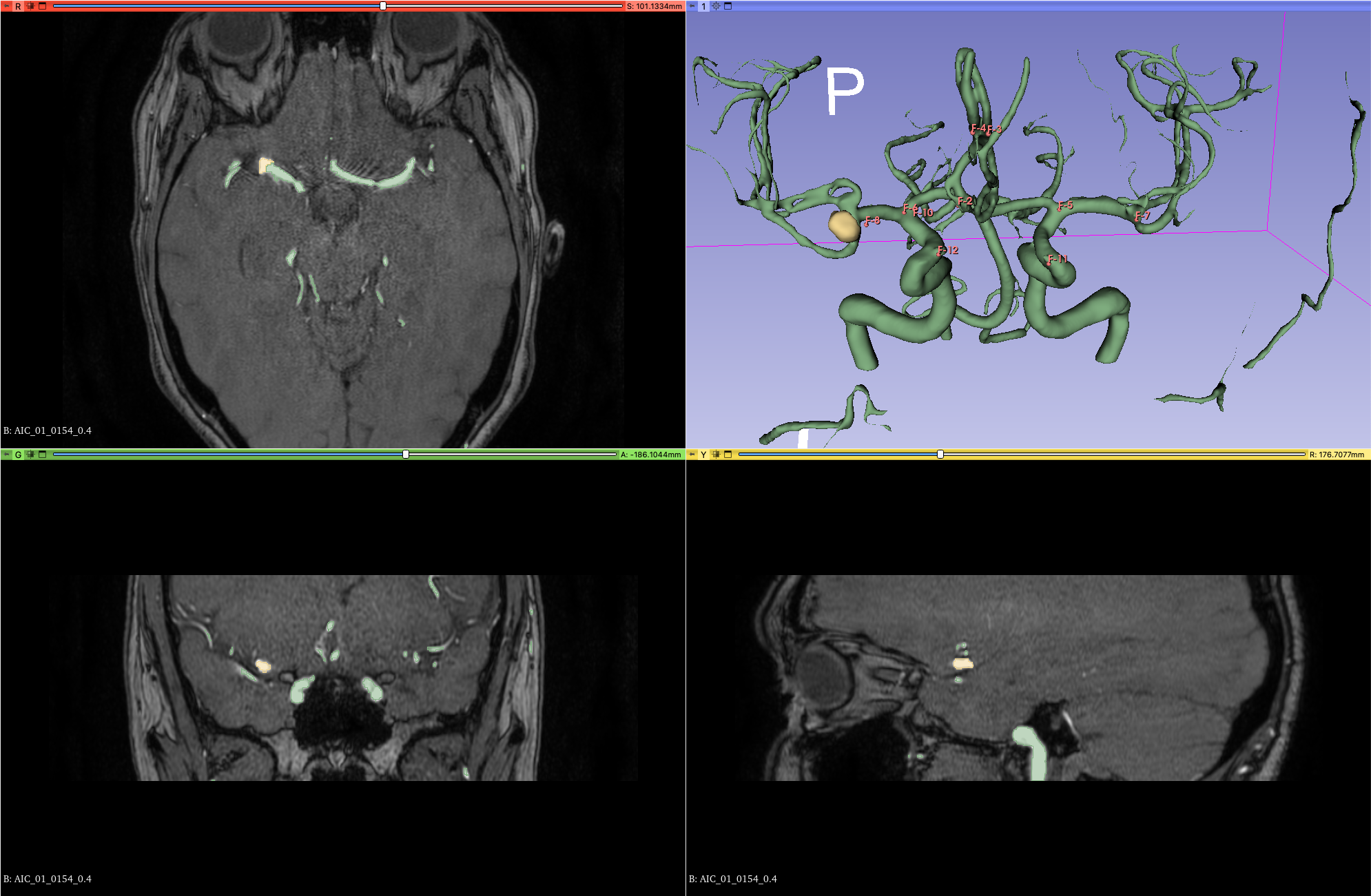
Using 3D Slicer, we have manually segmented 300 MRA-TOF images. Both the vascular tree, and the aneurysm (if any) were segmented. Moreover, we have also positioned Fiducials (or Markups) onto the 15 bifurcations of interest.

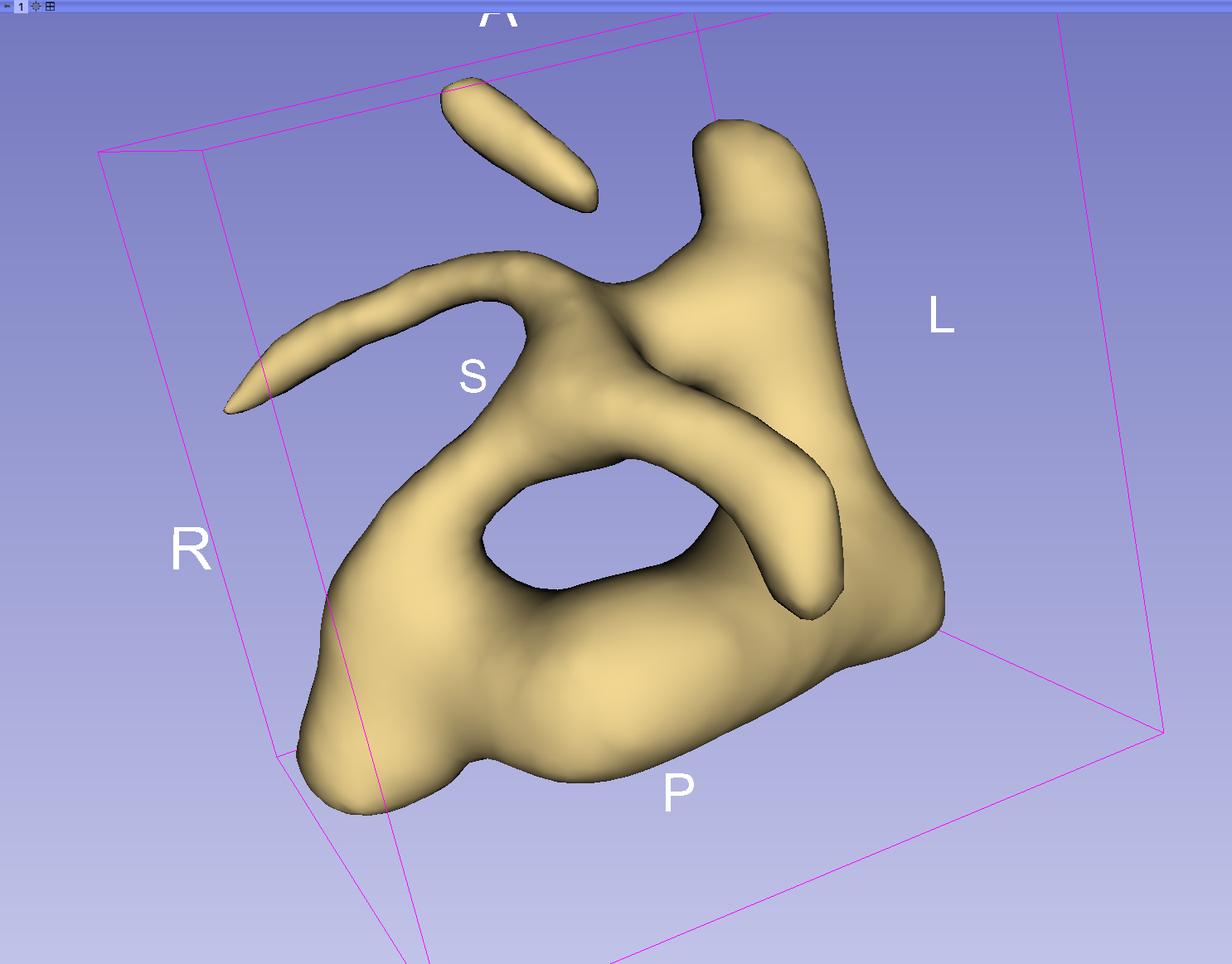
The figure below shows at the same time, the vascular tree segmentation (depicted in green), the aneurysm (in yellow) and the 15 bifurcations of interest (fiducials in red).

Thanks to this "Ground Truth" dataset, we can then run our vascular model on the 300 TOFs and thus generate tens of thousands of distorted versions of various portions of the MRA TOF images.

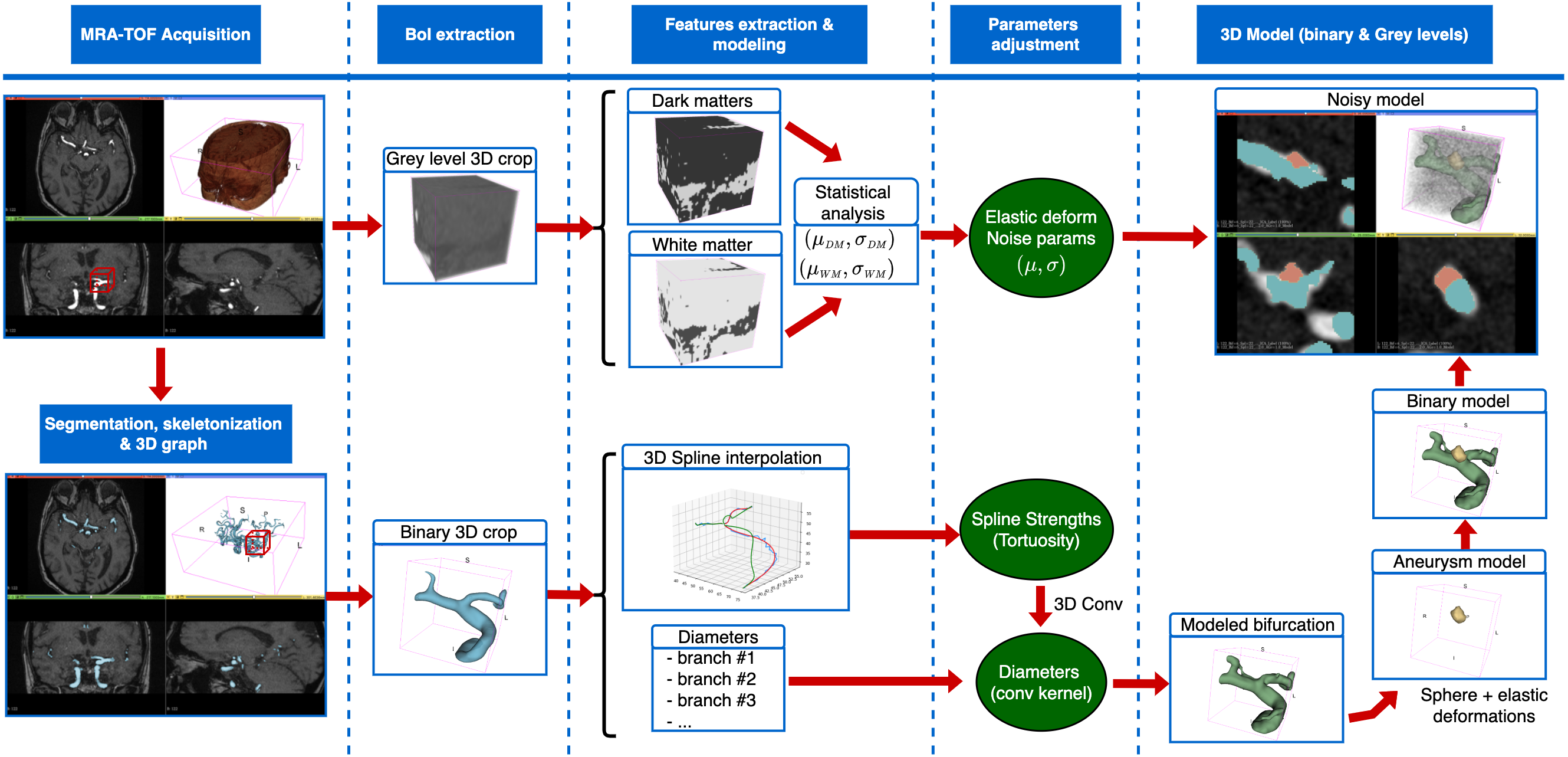
The synthetic Vascular Model operates as follows :

The upper branch of this schematic representation shows how we model the background noises (white/gray matters, cerebrospinal fluid, lateral ventricles, etc.), whereas the arterial tree modeling is depicted in the lower branch.

The noise modeling is relatively simple, we first generate some high frequency Gaussian noise, which will later on go through a Gaussian filter of specific properties, so as to end up having similar noise as our MRA-TOF target. The maths behind the noise generation process are summarized here.

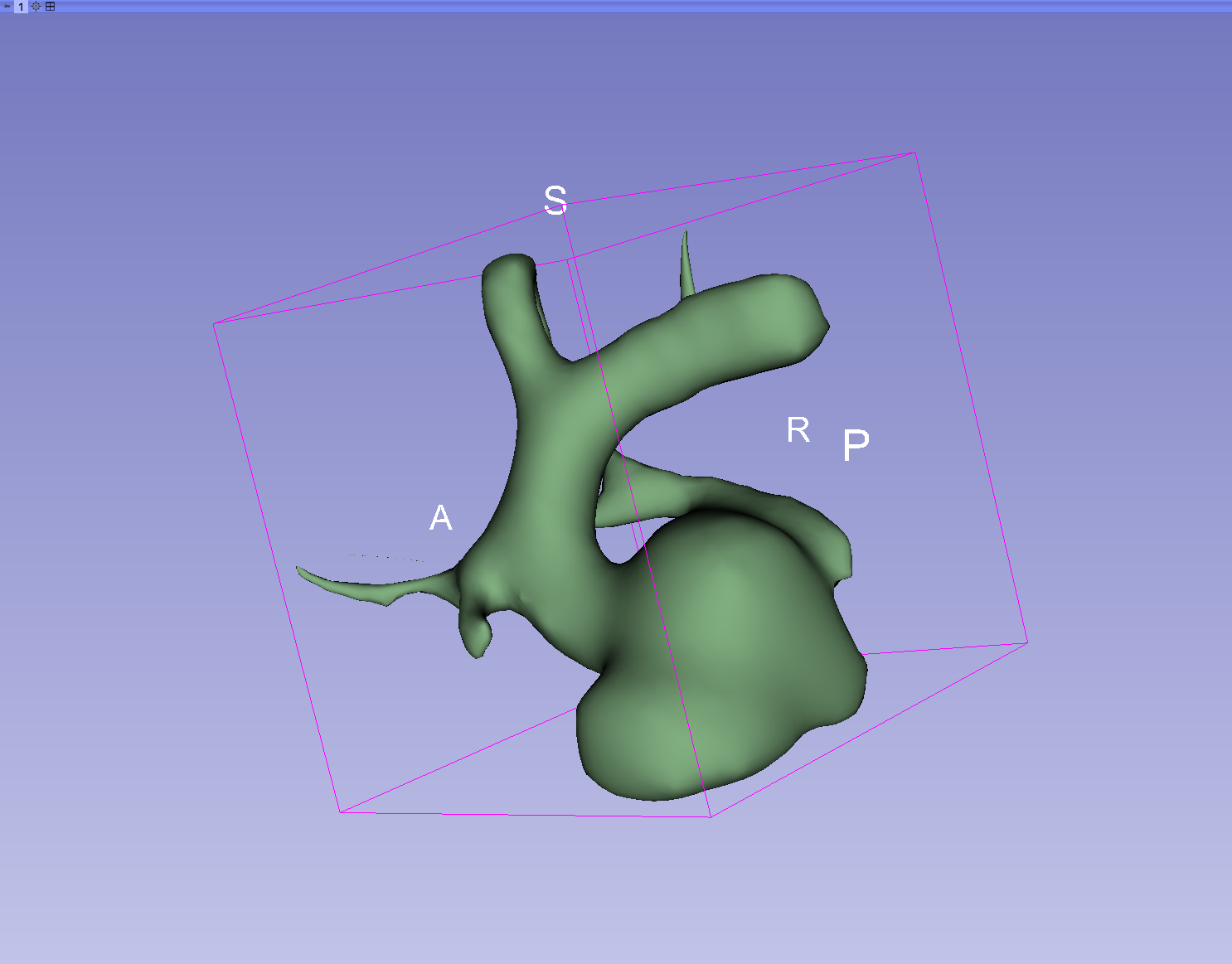
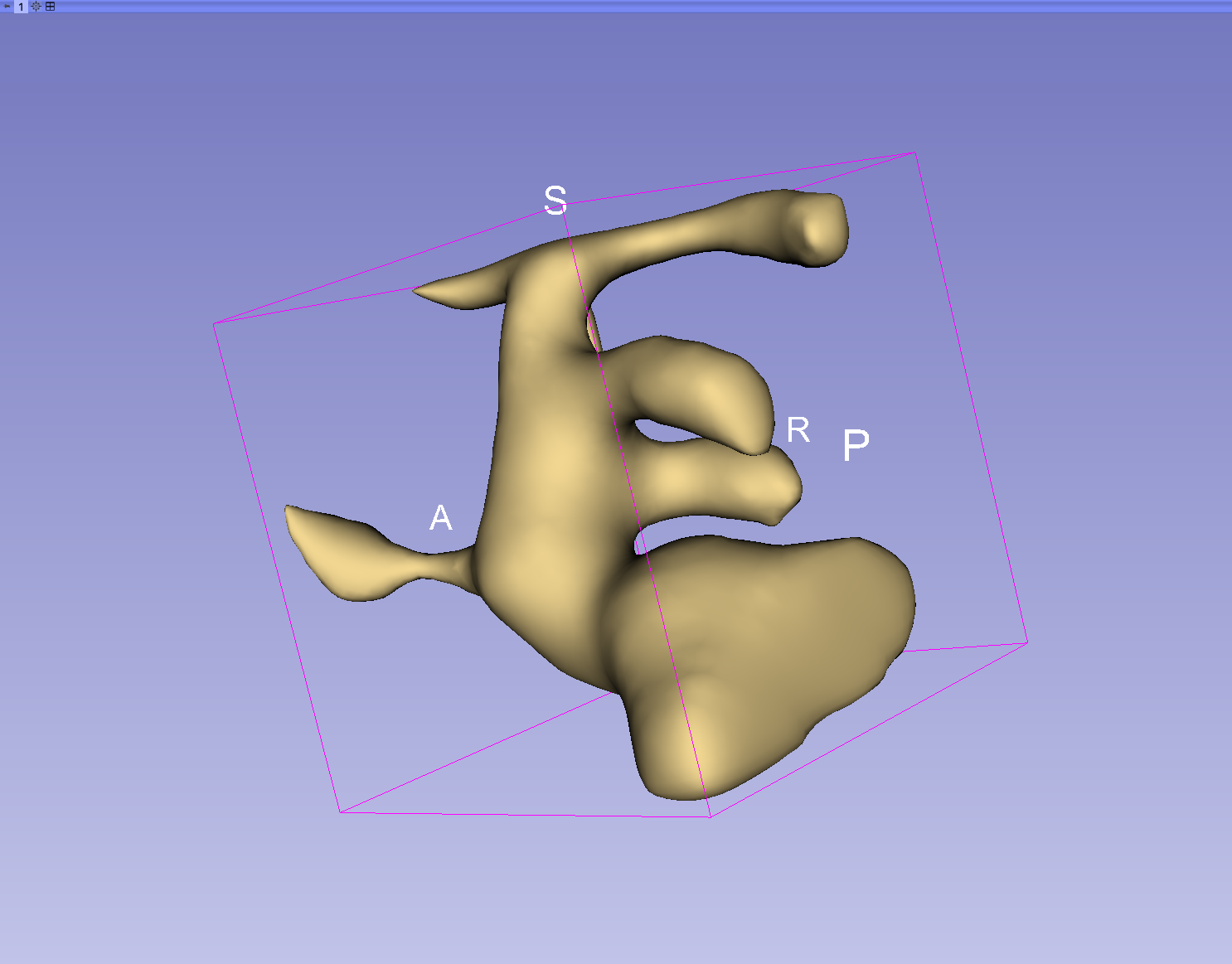
Concerning the modulation of the bifurcation geometry, this figure shows how altering the spline coefficients can help to tweak the arteries' tortuosity.

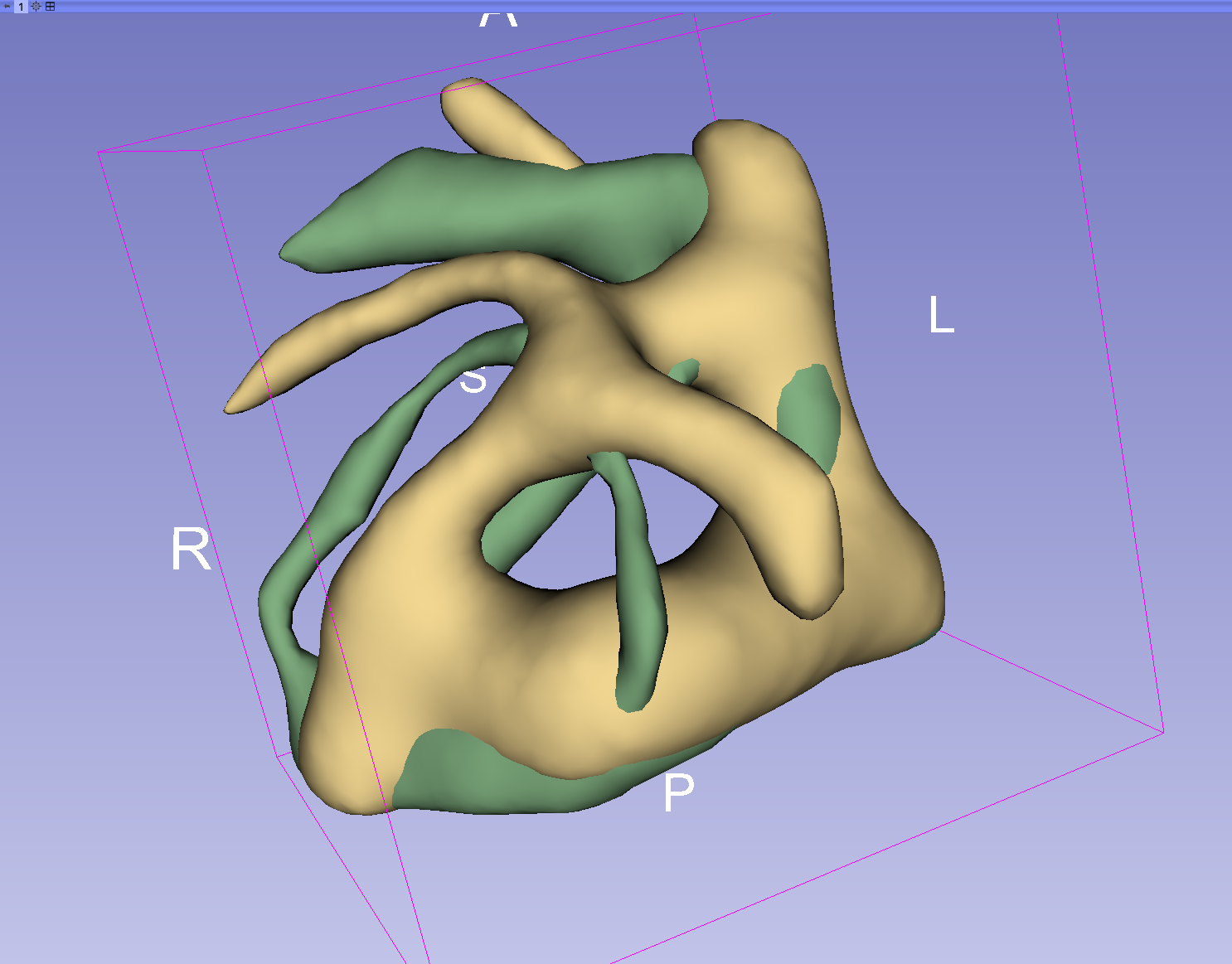
The figure below shows how the branches can be modified from the actual bifurcation (left images) to the modeled version (center images). The images in the right panels show the superimposition of both versions.

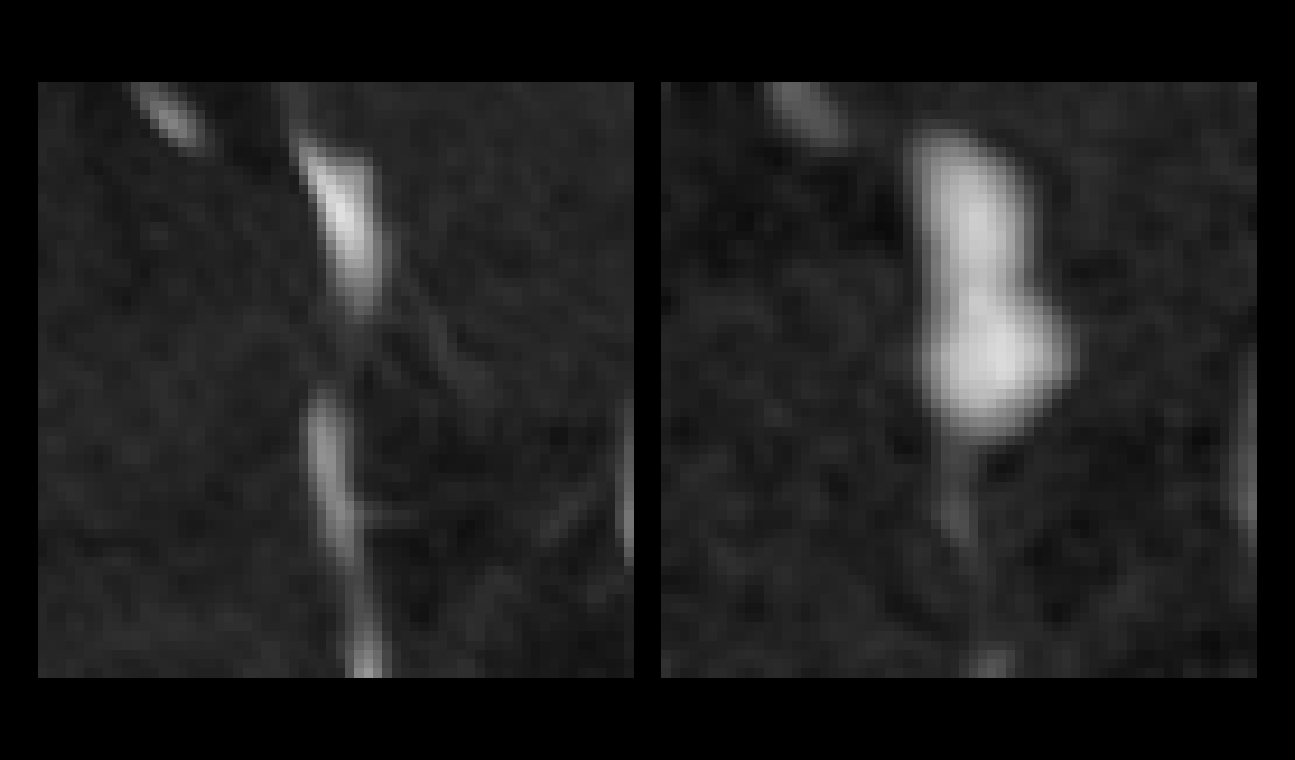
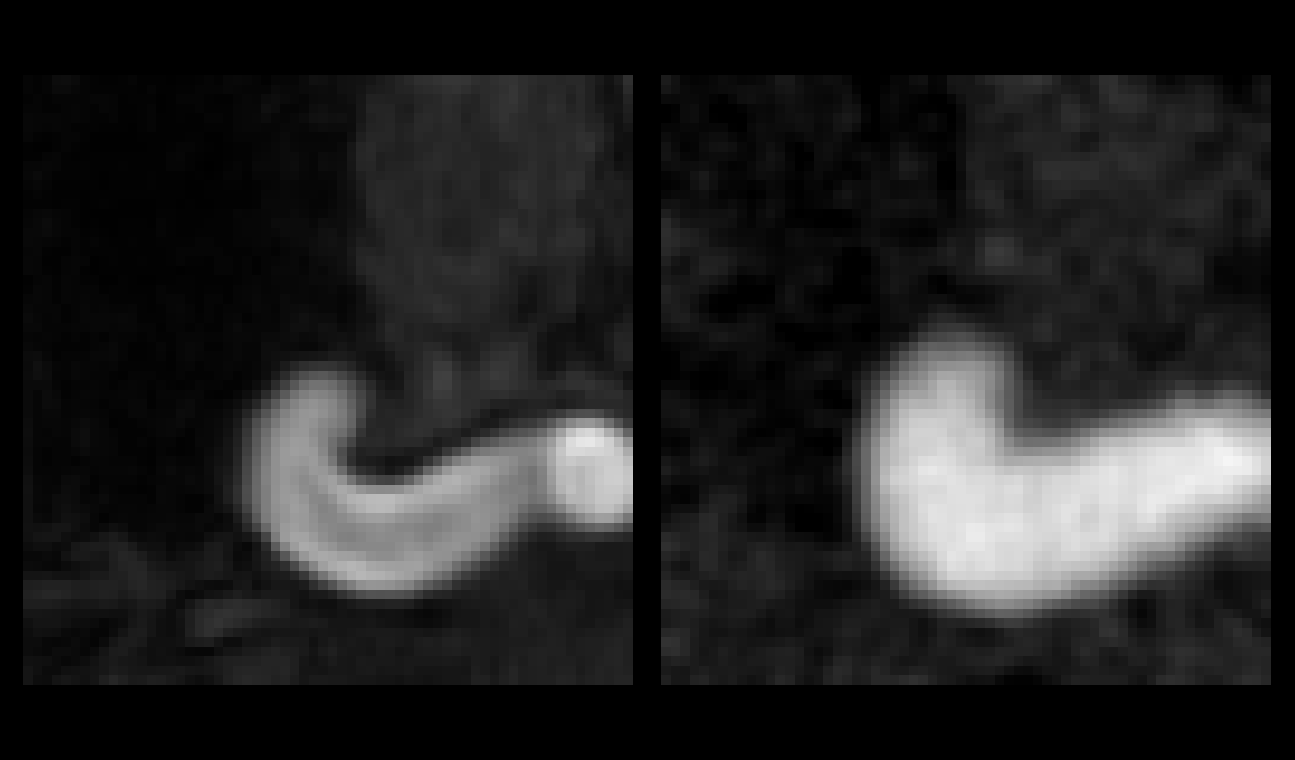
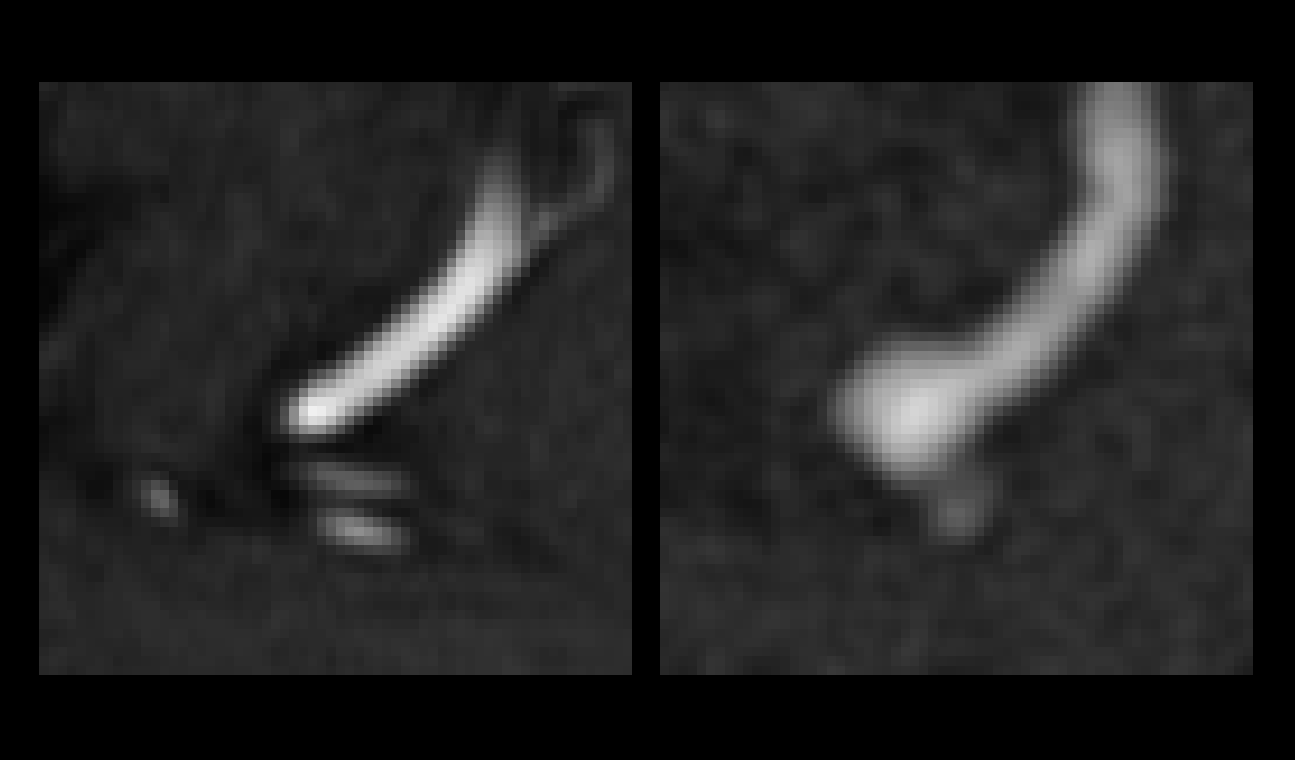
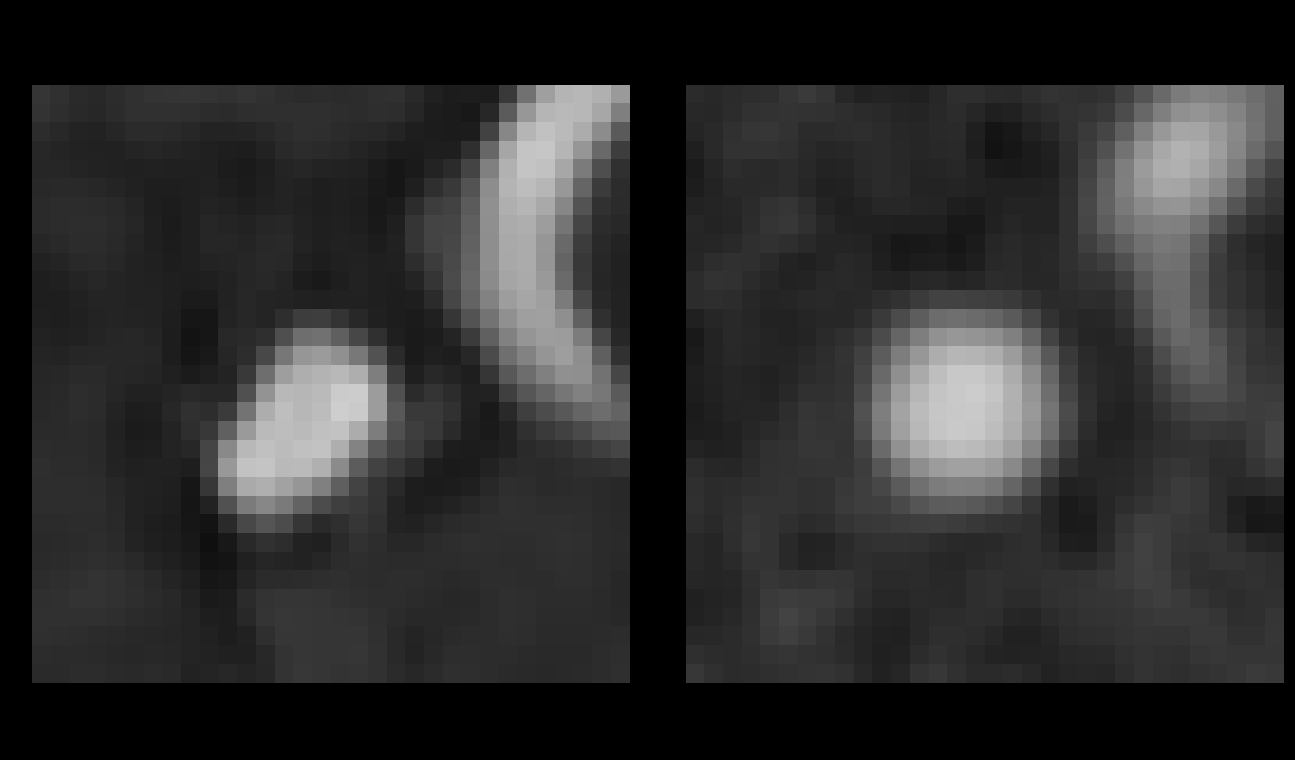
Some results :

The images below show some 2D slices along with the 3D representation of both bifurcations.

The 2D slices are represented on the left column of the figure, the ground truth TOF patches (GT) are depicted on the left, and their modeled versions are on the right.

As for the 3D representations (right column), the GT arteries are filled in white, whereas the modeled arteries are filled with yellow.

We can observe that both the arteries' shape and the background noise are very accurately modeled.

2D slices (GT vs Model)	3D representations

Finally, our model also allows to include an aneurysm in between the two daughter arteries (See figures below).

2D slices (GT vs Model)	3D representations

Again, the gray scaled images on the left represent both the original crop from the TOF acquisition (left) and its modeled version (right). In the 3D representations above, the green branch represents the mother artery, the aneurysm is depicted in blue.

Evidently, once an aneurysm has been detected, it goes through a full characterization step, i.e. we compute its bounding box, its volume, the elongation and flatness coefficients, the neck surface and a sphericity index (see this example).

The aneurysm is placed at distance D from the bifurcation center, such that :

r is the aneurysm radius, R is the average radius of the branches forming the bifurcation, and Θ stands for the angle formed by the two daughter arteries. This equation allows to automatically adjust the shift from the aneurysm center and the vessel wall where the daughter arteries split.

Related works

Patents

F. Autrusseau and R. Nader, "Method for Recognizing Bifurcations in a Vascular Tree, Associated Methods and Devices" , Patent EP 22305928.8, submitted on June 27th 2022.

F. Autrusseau, A. Nouri and R. Bourcier, "Methods for Segmenting Digital Images, Devices and Systems for the Same", Patent Eur. 20305143.8, submitted on Feb. 14th 2020.

A. Nouri, F. Autrusseau and R. Bourcier, "Method for Locating and Characterizing Bifurcations of a Cerebral Vascular Tree, Associated Methods and Devices", Subm. #EP18306612.5, Patent WO/2020/116162, submitted on Dec. 4th, 2019, published on June 11th 2020.

International Journals

I. Essadik, A. Nouri, R. Touahni, R. Bourcier, F. Autrusseau, "Automatic classification of the cerebral vascular bifurcations using dimensionality reduction and machine learning", in Elsevier Neuroscience Informatics, Sept. 2022.

J. Boucherit, B. Kerleroux, G. Boulouis, G. Tessier, C. Rodriguez-Regent, P. Sporns, H. Ghannouchi, E. Shotar, F. Gariel, G. Marnat, J. Burel, H. Ifergan, G. Forestier, A. Rouchaud, H. Desal, A. Nouri, F. Autrusseau, G. Loirand, R. Bourcier, V. L’Allinec, "Bifurcation geometry remodelling of vessels in de-novo and growing intracranial aneurysms: A multicenter study", in Journal of NeuroInterventional Surgery, 2022.

A. Nouri, F. Autrusseau, R. Bourcier, A. Gaignard, V. L’Allinec, C. Menguy, J. Veziers, H. Desal, G. Loirand and R. Redon, "Characterization of 3D Bifurcations in Micro-scan and MRA-TOF Images of Cerebral Vasculature for Prediction of Intra-Cranial Aneurysms", in Elsevier Computerized Medical Imaging and Graphics (CMIG), DOI, 14th July 2020.

V. L’Allinec, S. Chatel, M. Karakachoff, E. Bourcereau, Z. Lamoureux, A. Gaignard, F. Autrusseau, S. Jouan, A.C. Vion, G. Loirand, H. Desal, O. Naggara, R. Redon, M. Edjlali and R. Bourcier, "Prediction of Unruptured Intracranial Aneurysm Evolution: The UCAN Project", in Neurosurgery, Oxford University Press, Feb. 2020.

International Conferences

F. Autrusseau, R. Nader, A. Nouri, V. L'Allinec, R. Bourcier, "Toward a 3D Arterial Tree Bifurcation Model for Intra-Cranial Aneurysm Detection and Segmentation", in Intl. Conf. on Pattern Recog, ICPR'22, Montreal, Canada, Aug. 21-25 2022.

I. Essadik, A. Nouri, N. Lauzeral, R. Touahni, R. Bourcier, F. Autrusseau, "Combining machine learning and artery characterization to identify the main bifurcations in 3Dvascular trees", in SPIE Medical Imaging 2022, San Diego, CA USA, 20 - 24 Feb. 2022.

S. Chater, N. Lauzeral, A. Nouri, Y. El Merabet, F. Autrusseau, "Learning from mouse CT-Scan brain images to detect MRA-TOF human vasculatures", in 43rd International Conf. of the IEEE Engineering in Medicine and Biology Society, IEEE EMBC, 1 - 5 Nov. 2021.

J. Guillou, F. Autrusseau, R. Bourcier, "Brain Vasculature Segmentation based on Human Perception Criteria", in SPIE Medical Imaging 2020, Houston, TX USA, 15 - 20 Feb. 2020.

A. Nouri, F. Autrusseau, R. Bourcier, A. Gaignard, V. L'Allinec, C. Menguy, J. Veziers, H. Desal, G. Loirand, R. Redon, "3D bifurcations characterization for intra-cranial aneurysms prediction", in SPIE Medical Imaging 2019, San Diego, CA USA, 16 - 21 Feb. 2019.

Website template by Arcsin